Chapitre 26
Les Opérations sur la Matière
et le Vide
Opérations Booléennes
![]()
Retour au sommaire principal
1 - Opérations sur la matière et le Vide
1 - Introduction
Les Booléennes, ou Booliènnes, sont des opérations relatives aux théories de Georges BOOLE, logicien et mathématicien britannique (1815-1864).
Soit C l'objet résultant d'une opération entre deux objets A et B. L'opérateur booléen de 3D Turbo NT comporte 10 opérations :
|
|
l'union (ou fusion) de 2 solides A et B |
C = A U B
|
|
|
l'intersection de 2 solides A et B |
C = A ∩ B
|
|
|
la soustraction de 2 solides A et B |
C = A - B C = B - A |
|
|
la soustraction ouverte de 2 solides A et B |
C = A - B C = B - A |
|
|
la soustraction sur l'enveloppe, peau de A la soustraction sur l'enveloppe, peau de B |
C = A - B C = B - A |
|
|
la section commune - Profil d'intersection (ET exclusif) |
C = A et B
|
|
|
la différence symétrique de 2 solides A et B (OU exclusif) |
C = A xor B
|
2 - La Matière
Avec les opérations booléennes, 3D Turbo NT est non seulement un logiciel 3D "surfacique" mais également un logiciel 3D "volumique", ce qui signifie qu'il faut raisonner "Matière" et "Antimatière".
Les opérations booléennes de 3D Turbo NT fonctionnent sur les volumes (surfaces fermées) et les surfaces ouvertes.
La "Matière" n'existe que par rapport à "l'Antimatière", le "Plein" par rapport au "Vide",. "l'Intérieur" par rapport à "l'Extérieur". "Matière, Plein, Intérieur" sont des synonymes désignant la partie solide d'un objet. "Antimatière, Vide, Extérieur, Creux, Poche" sont des synonymes désignant l'espace dépourvu de matière.

L'enveloppe (ou peau) délimite l'intérieur de l'extérieur.
Cette partie n'a aucune épaisseur. Elle permet simplement de représenter la matière. Dans 3D Turbo NT, cette partie est appelée "Surface", d'où le qualificatif de "Surfacique" quand la notion de "Solide" n'existe pas.

Dans 3D Turbo NT, c'est l'orientation des "Normales" aux surfaces qui différencie le coté matière du côté antimatière :

3 - Définition des opérations booléennes
Par "solide", nous désignons la matière de l'objet, pour faire ressortir la notion de "peau" qui n'est que le reste de l'enveloppe de l'un des deux objets.

Soit deux objets A et B, dont les normales sont orientées vers l'intérieur, donc des objets solides.
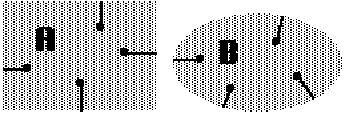
|
Union de solides# |
||
|
|
1 - Union de solides - Addition Booléenne |
|
L'union ou fusion de A et B, notée A U B (A union B), est formée des éléments de l'ensemble C qui appartiennent à A ou à B (à au moins l'un des deux).
|
|
|
|
Intersection de solides# |
||
|
|
2 - Intersection de solides - Partie commune |
|
L'intersection de A et B, notée A ∩ B (A inter B), est formée des éléments de l'ensemble C qui appartiennent à la fois à A et à B (ensemble des éléments communs).
|
|
|
|
Soustraction de solides# |
||
|
|
3 - Soustraction de solides. |
|
La différence (ou soustraction) entre A et B, notée A - B (A moins B), est formée des éléments de C qui sont eux-mêmes :
|
|
|
|
Soustraction sur l'enveloppe# |
||
|
|
4 - Soustraction sur l'enveloppe - Peau de A-B |
|
La différence (ou soustraction) entre A et B, notée A - B (A moins B), est formée des éléments de C qui sont eux-mêmes :
|
|
|
|
Soustraction Inverse sur l'enveloppe# |
||
|
|
5 - Soustraction Inverse sur l'enveloppe |
|
|
|
|
|
Profil d'intersection# |
||
|
|
6 - Section commune (ET exclusif) - Profil d'intersection |
|
La section commune entre A et B, notée A et B, est formée des éléments de l'ensemble C qui appartiennent à la fois aux deux objets A et B.
|
|
|
|
Différence symétrique de solides# |
||
|
|
7 - Différence symétrique de solides (OU exclusif) |
|
La différence symétrique de A et B, notée A xor B, est formée des éléments de l'ensemble C qui appartiennent à l'un des deux objets A ou B et à un seul.
|
|
|
4 - Importance du sens matière
La notion de "Matière" et "d'Antimatière" a une importance primordiale dans le résultat des opérations booléennes.
Voici un exemple de fusion sur deux objets A et B.
La combinaison des cas d'orientations de leurs normales offre quatre résultats différents:




Une sphère dont les normales sont orientées vers l'extérieur, représente en réalité un cube infini, avec une poche sphérique (vide) en son milieu.
N'ayant pas d'autre moyen pour représenter cet infini, nous dessinons ce qui a une échelle humaine "la poche".
C'est en fonction de cette contrainte que les objets créés dans 3D Turbo NT par une opération booléenne sont différents.
Si les normales des deux objets A et B sont orientées vers l'intérieur, c'est à dire que l'enveloppe dessinée représente l'extérieur des objets, la fusion qui en résulte s'appréhende aisément.
Par contre, dans les trois autres cas, il faut penser constamment qu'on ne peut représenter que le "Vide" qui en résulte, d'ailleurs c'est aussi la représentation de l'extérieur des objets.
5 - Constitution des Solides
Les éléments géométriques mis en œuvre dans les opérations booléennes doivent répondre à des critères topologiques rigoureux, faute de quoi l'opérateur de calcul risque de produire des erreurs ou des résultats inattendus.
Les critères suivants doivent impérativement être respectés. Toute erreur produite par une opération booléenne doit conduire l'opérateur à vérifier immédiatement la validité des objets impliqués dans l'opération.
Critères de constitution des solides
Les objets utilisés dans une opération booléenne doivent remplir les conditions suivantes :
|
|
|
Un objet ouvert est un objet dont la peau présente un trou.
Ca peut être un objet fermé à l'origine, dont on a enlevé une ou des facettes.
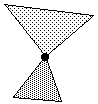
Ca peut être également un objet ayant deux arêtes superposées, (objet de révolution comme une sphère, avec profils 0 et 360 superposés) :
Remarque : Certains objets constitués de plusieurs solides, peuvent être parfois considérés soit comme "OUVERTS" soit comme "FERMÉS", le résultat n'étant pas du tout le même.
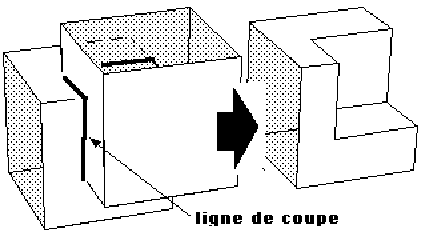
Soit un objet (A) constitué de deux cubes, ayant une facette adjacente, dont les points sont doublés :
|
|
|
Si on supprime l'une des deux facettes centrales, l'objet (A) peut être soit "OUVERT" soit "FERMÉ".
Voici le résultat d'une fusion entre les objets (A et B) si (A) est déclaré fermé.
Le logiciel en apprenant la forme de l'objet (A) a ignoré la partie de gauche, considérant qu'elle n'était pas cohérente avec le reste.
|
|
|
|
Voici le résultat d'une fusion entre les objets (A et B) si (A) est déclaré ouvert.
L'orientation de la facette centrale n'a pas d'importance, car le logiciel la corrige de lui-même.
|
|
|



|
Orientation Automatique des Normales# |
||
|
|
1 - Orientation Automatique des Normales |
|
Après qu'un objet a été créé par la voie géométrique ou surfacique, il est parfois nécessaire d'homogénéiser l'orientation des normales de ses facettes en vue de son utilisation par les opérations booléennes, ou pour un rendu photoréaliste.
Vérifier que les normales aient bien été orientées dans le sens matière désiré, sinon inverser toutes les normales de l'objet.
|
Vérifier un objet# |
||
|
|
2 - Vérifier un objet |
|
Après qu'un objet a été créé par la voie géométrique ou surfacique, ou après qu'une opération booléenne a donné un résultat inattendu ou une erreur, il est nécessaire de vérifier s'il répond aux critères topologiques requis pour son utilisation en vue de son utilisation par les opérations booléennes.
Observer la création de nouveaux objets de type CNX. Ils représentent :
Vérifier si les objets CNX sont normaux et acceptables (objets multi-composants) ou bien s'il s'agit de parties indésirables (cloisons,..)
Si des parties CNX sont jugées indésirables :
|
Nettoyer un objet# |
||
|
|
3 - Nettoyer un objet |
|
Si un objet contient des éléments détectés comme topologiquement inacceptables (cloisons CNX, etc), cette fonction va séparer ces éléments de l'objet et les mettre dans un autre objet de type CNX.
A l'issue de cette opération, l'objet initial aura donc été nettoyé de ses éléments indésirables et sera considéré comme bon pour les opérations booléennes.
|
Réaliser une Opération Booléenne# |
||
|
|
1 - Réaliser une Opération Booléenne |
|
Pour réaliser une opération booléenne, préparer 2 objets répondant strictement aux critères et restrictions énoncés plus haut.
En suivant les indications affichées dans la barre d'états :
Remarque : Si un objet est hiérarchique, cliquer un des ses points pour le sélectionner peut conduire à sélectionner un de ses fils et non pas l'objet père lui-même. Pour résoudre ce problème, activer le mode de validation du choix des objets décrit dans le paragraphe Réglage des fonctions interactives du chapitre Créer des Entités.
Le dialogue suivant est proposé :

Les cases à cocher ouvert sont renseignées pour information, selon que les objets désignés ont été détectés comme étant ouverts ou non.
Les objets générateurs ne sont jamais effacés ni modifiés.
Les calculs sont animés à l'écran.
On peut observer les différentes phases de l'opération :
Sélectionner le calque destination en mode Courant et observer le résultat.
Si ce résultat ne correspond pas à ce qui est attendu :
ou
L'une des dispositions ci-dessus suffit très souvent à régler une situation d'erreur.
|
Charte des Opérations Booléennes# |
||
|
|
2 - Charte des Opérations Booléennes |
|
Le tableau ci dessous indique le résultat des opérateurs booléens en fonction du sens matière des objets.
|
|
|
|
|
|
|
|
|
|
|
Opération |
A U B |
A ∩ B |
A - B |
B - A |
A - B ouvert |
B - A ouvert |
A - B peau |
B - A peau |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Les opérations de calcul de profil et de OU exclusif génèrent toujours le même résultat et ne sont donc pas représentées dans ce tableau.
|
Exemples d'Opérations Booléennes# |
||
|
|
3 - Exemples d'Opérations Booléennes |
|
Voici plusieurs exemples du rôle fondamental de l'orientation des facettes dans le résultat d'une opération de FUSION :
Union (ou fusion) entre deux cubes :



Union (ou fusion) entre une pyramide et un cube :



Union (ou fusion) entre deux cylindres :



Union (ou fusion) entre un cube et un cylindre :



Union (ou fusion) entre une pyramide et un cylindre :



Union (ou fusion) entre un cylindre et un cône :

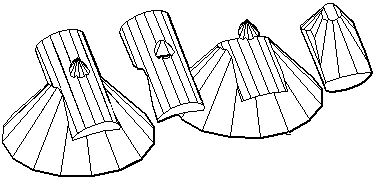

Exemple de sections - Profil d'intersection
La section contient des points qui appartiennent à la fois à l'objet A et à l'objet B.
Elle peut servir comme parcours pour un tubage.
L'opérateur produit toujours 2 profils strictement superposés, un pour chaque objet.
Il est nécessaire de fusionner ces profils à l'aide de la fonction d'optimisation du modèle appliquée au calque contenant les profils.


Opérations booléennes entre un plan et un tore :


Opérations entre une sphère pleine et une pile de plans aux normales alternées :
|
|
|
|
|
|
|
|
|
|
|
Raccordement d'un Volume et d'une Surface (Soustraction A-B) :
|
|
|
Percement d'un Mur par Objet Disjoint
(Soustraction A-B) :
|
|
|
Passage routier dans un modèle numérique de terrain :


